ARIMA模型原理及实现
ARIMA模型原理及实现
参考资料
- arma 数理方法 时间序列分析、常用统计软件及应用
导包
1
2
3
4
5
6
7
8
9
10
11
12
13
14import warnings
warnings.filterwarnings("ignore") # 不再显示warning
import pandas as pd
import matplotlib.pyplot as plt
# from matplotlib import qq
import datetime
import torch
import torch.nn as nn
import numpy as np
from torch.utils.data import Dataset, DataLoader
import os
os.chdir(os.getcwd())
plt.rcParams['font.sans-serif'] = ['SimHei'] # 处理中文显示问题
通过 baostock 包提供的接口获取训练数据集
1 | import baostock as bs |
获取数据集
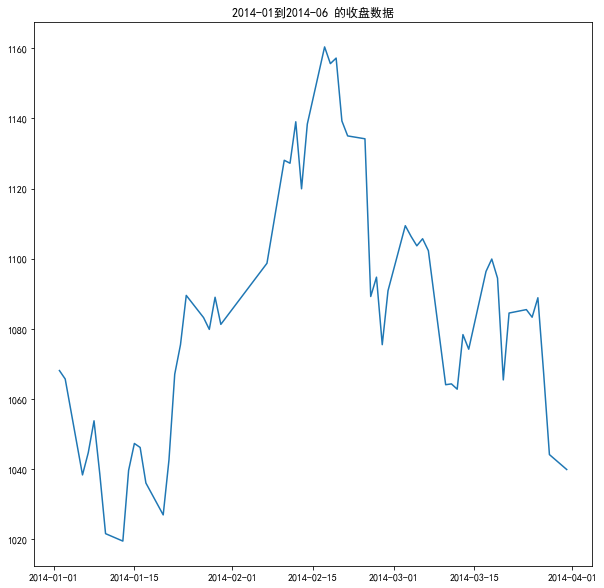
1 | getIndexDate(code='sz.399106',start_date='2014-01-01', end_date='2014-12-01') |
处理
1 | import pandas as pd |
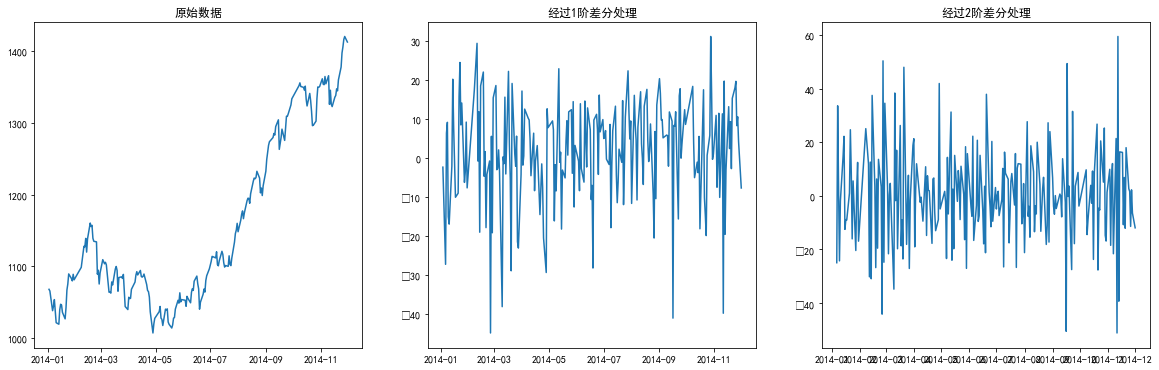
差分处理
1 | ChinaBank['Close_diff_1'] = ChinaBank['Close'].diff(1) |
计算: AIC BIC
1 | train_results = sm.tsa.arma_order_select_ic(train, ic=['aic', 'bic'], trend='nc', max_ar=4, max_ma=4) |
output
1 | AIC (1, 0) |
模型检验
1 | model = sm.tsa.ARIMA(train, order=(1, 0, 0)) |
做D-W检验
1 | 德宾-沃森(Durbin-Watson)检验。 |
input
1 | sm.stats.durbin_watson(results.resid.values) |
output
1 | 1.802970716007886 |
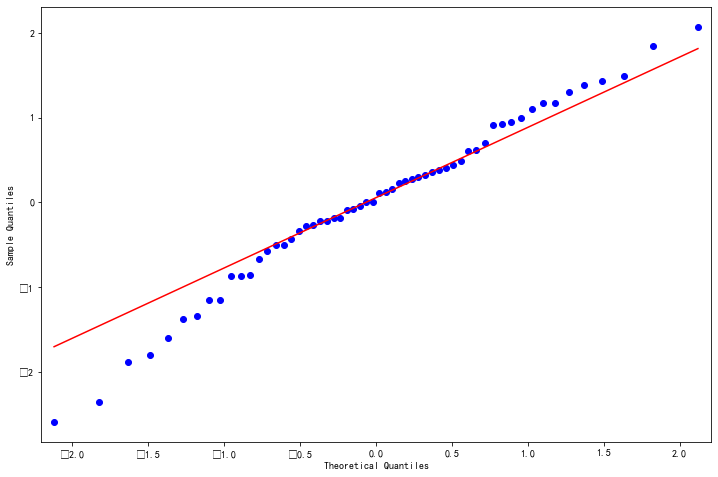
观察是否符合正态分布,QQ图
1 | 这里使用QQ图,它用于直观验证一组数据是否来自某个分布, |
1 | from statsmodels.api import qqplot |
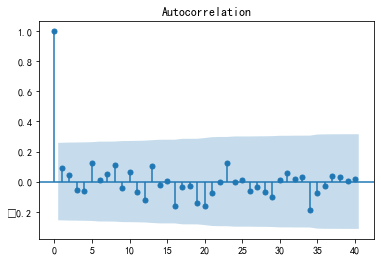
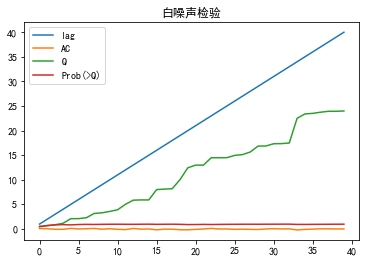
Ljung-Box检验(白噪声检验)
1 | Ljung-Box test是对randomness的检验,或者说是对时间序列是否存在滞后相关的一种统计检验。 |
input
1 | r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True) |
结果分析:
1 | 原假设为白噪声(相关系数为零) |
就结果来看:
1 | 如果取显著性水平为0.05或者0.1,结果不小于显著性水平,那么相关系数与零没有显著差异,即为白噪声序列 |
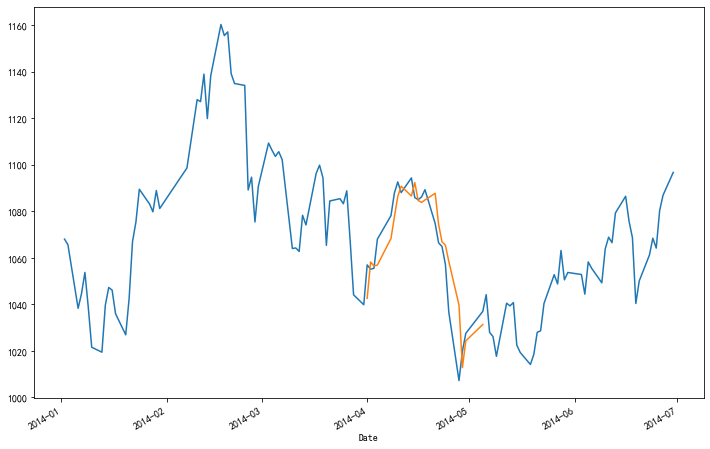
模型预测
1 | model = sm.tsa.ARIMA(sub, order=(1, 0, 0)) |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Jacker-zzk's Blog!